Konvoluce je operátor, který ze dvou funkcí vytvoří funkci novou. Pro dvourozměrný případ ve spojitém prostoru vypadá následovně \[ (f*g)(x, y) = \int_{u=-\infty}^{\infty} \int_{v=-\infty}^{\infty} f(x-u, y-v) g(u, v) dudv \] V článku se ovšem budeme zabývat diskrétním tvarem, který použijeme na zpracování rastrového obrazu a který nám ve vztahu výše umožní nahradit integrály sumami.
Použití
Obrázky níže ukazují možné aplikace.
| | |
| a) | b) | c) |
| | |
| d) | e) | f) |
| a) vstupní obrázek; b) rozostření; b) zaostření; c) detekce hran; d) detekce vertikálních hran; e) detekce horizontálních hran |
Jak vidíme, dokážeme tímtéž algoritmem dosáhnout velmi odlišných výstupů. Každý pak může být zajímavý ať už vizuálním dojmem, nebo z hlediska další aplikace.
Algoritmus
Mějme vstupní obrázek a jeden další velikosti $n*n$. Tomu budeme říkat maska a ono $n$ bude nejčastěji 3. Na obrázku můžete vidět graficky, co potřebujeme pro použití konvoluce.
| \[\left( \begin{array}{ccc} 76 & 107 & 45 \\ 168 & 150 & 224 \\ 104 & 145 & 114 \end{array} \right)\] |
| a) | b) |
| \[\left( \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right)\] |
| c) |
| a) vstupní obrázek; b) intenzity pixelů vstupního obrázku; b) maska |
Masku položíme na obrázek a bod který leží pod jejím středem, budeme počítat. Jednoduše vynásobíme hodnotu jasu daného pixelu hodnotou masky, která mu svým překrytím odpovídá. Všechny takové hodnoty (pro masku $3*3$ jich bude 9) sečteme a dostaneme novou hodnotu pro náš počítaný pixel. Poté okno přesuneme na další bod a počítáme dále. Mějme na paměti, že pro obraz s více barevnými kanály než jedním, počítáme konvoluci pro každý kanál zvlášť.
Matematicky
Popišme si algoritmus matematicky. Následující vztah definuje diskrétní dvourozměrnou konvoluci \[ I(x,y)=\sum_{i=-k}^{k}\sum_{j=-k}^{k} f(x-i,y-j)\cdot g(i,j) \] kde $I(x,y)$ značí intenzitu výsledného pixelu na pozici $[x,y]$, $f(x,y)$ je intenzita vstupního obrázku na pozici $[x,y]$ a $h(i,j)$ intenzita bodu v masce na pozici $[i,j]$. Zkusme si spočítat příklad z obrázku výše. Počítáme bod $[1,1]$ (tedy ten uprostřed). Masku máme velkou 3*3 pixely, takže její indexy budou v každém směru $-1,0,1$ a $k=1$. Ve výrazu máme dvojitou sumu, ze které vidíme, že budeme sčítat 9 čísel. Zapišme si první část, kdy vypočítáme první z řady a to pixel vpravo dole. Indexy $i$ a $j$ se tedy pro první průchod budou rovnat \[ i=-k=-1 \] \[ j=-k=-1 \] po dosazení do vzorce dostaneme při středu $[1,1]$ pro políčko vpravo dole hodnotu \[ \begin{array}{lcl} I_{vd}(1,1)&=&f(1-(-1),1-(-1))\cdot h(-1,-1) \\ &=&f(2,2)\cdot h(-1,-1) \\ &=&114\cdot 1 \\ &=&114 \end{array} \]
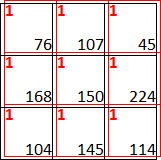
Jak můžete vidět, pro políčko vpravo dole v původním obrázku používáme políčko vlevo nahoře v masce. Mějte na paměti, že
se maska při použití otočí horizontálně a vertikálně! Po dokončení výpočtu dostaneme hodnotu prostředního pixelu v rámci konvoluční masky. \[ I(1, 1)=76+107+45+168+150+224+104+145+114=1133 \] Vypočítaná hodnota značně přesahuje maximální intenzitu barevného kanálu, což nedokážeme vykreslit. Nabízí se řešení nahradit vyšší čísla maximální hodnotou 255. V tomto případě není řešení vhodné. Každý pixel ve vstupním obrázku je ohodnocen hodnotou v masce, která mu přiřadí jeho důležitost v daném okolí. Pro příklad uvažujme obrázek $300*200$ v šedé barvě, kde má každý pixel jas 125. Po aplikaci masky uvedené výše by každý pixel obrazu nabyl hodnoty $9*125=1125$. Kdybychom se rozhodli velké hodnoty jednoduše nahradit nejvyšší možnou intenzitou, což je 255, dostali bychom bílý obdelník. Jak vidíme, výsledek rozostření šedého obrázku by pravděpodobně neměl být obrázek bílý. Zkusme vyzkoušet, co se stane když se zaměříme pouze na poměr hodnot v masce a na jejich součet. Nechejme všechny hodnoty stejné a trvejme na podmínce jejich součtu, který musí být roven jedné. Dostaneme tedy pole $3*3$ kde v každé buňce bude $1/9$. Po aplikaci této masky na náš šedý obrázek, dostaneme zpět tentýž. Přidáme tedy k výpočtu intenzity jeden krok, kdy výslednou hodnotu vydělíme součtem hodnot v masce. Tomuto procesu se říká normalizace a budeme ho provádět při konvoluci vždy, když bude součet hodnot v masce větší než jedna.
Implementace
Schématicky může implementace vypadat takto.
vahy = 0;
for(i = -K; i <= K; i++) {
for(j = -K; j <= K; j++) {
vahy += maska[1+i][1+j];
}
}
if (vahy < 1) vahy = 1;
for(radek = 0; radek < VYSKA; radek++) {
for(sloupec = 0; sloupec < SIRKA; sloupec++) {
soucet = 0;
for(i = -K; i <= K; i++) {
for(j = -K; j <= K; j++) {
intenzita = vstupni(radek + i, sloupec + j);
soucet += intenzita * maska[1+i][1+j];
}
}
vystupni(radek, sloupec) = round(soucet/vahy);
}
}
V principu potřebujeme dostat součet všech násobků pixelů v masce
maska spolu s odpovídajícími pixely ve vstupním obrázku
vstupni. Vypočítanou hodnotu poté vydělíme součtem hodnot v masce (normalizace). Všimněte si, že nová hodnota je vložena do nového obrázku
vystupni. Toto je velice důležité! Kdyby byla vložena do
vstupni , každá další hodnota by v sobě zahrnovala výpočet s už zpracovaným pixelem. Počítáme tedy s hodnotami z původního obrázku a nové vkládáme do jiného.
Různé masky
Na závěr článku se vraťme k obrázkům v první podkapitole a ukažme, jaké masky byly použity pro jejich vytvoření.
| \[\left( \begin{array}{ccc} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{array} \right)\] | Gaussův filtr |
| \[\left( \begin{array}{ccc} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \end{array} \right)\] | zvýraznění hran |
| \[\left( \begin{array}{ccc} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{array} \right)\] | operátor Laplace |
| \[\left( \begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array} \right)\] | Sobelův operátor (svislé hrany) |
| \[\left( \begin{array}{ccc} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{array} \right)\] | Sobelův operátor (vodorovné hrany) |
Poznámka Na spodní tři obrázky byla použitá dodatečná úprava. K intenzitě každého pixelu byla v každém kanálu přidána hodnota 128.
Literatura a odkazy
HLAVÁČ, V.; SEDLÁČEK, M. Zpracování signálu a obrazu. Vydavatelství CVUT, 2005. KOLCUN, A. Základy počítačovej grafiky. Učební texty, Ostrava 2006. ŽÁRA, J.; SOCHOR, J.; BENEŠ, B.; FELKEL, P. Moderní počítačová grafika. Computerpress, Brno 2004.
http://cs.wikipedia.org/wiki/Konvoluce http://bruxy.regnet.cz/fel/36ACS/konvoluce.pdf http://www.songho.ca/dsp/convolution/convolution2d_example.html http://homepages.inf.ed.ac.uk/rbf/HIPR2/convolutiondemo.htm - applet































